MATPOWER Interface#
See also the API reference for andes.interop.matpower.
import andes
from andes.interop.matpower import (start_instance,
to_matpower, from_matpower)
Create an Octave/MATLAB instance#
m = start_instance()
Convert to MATPOWER#
ss = andes.system.example() # load an ieee14 example case
mpc = to_matpower(m, 'mpc', ss)
Test if the power flow of mpc can be solved
m.eval("runpf(mpc)")
warning: error caught while executing handle class delete method:
'osqp_mex' undefined near line 40 column 13
OSQP Error!
MATPOWER Version 7.1, 08-Oct-2020 -- AC Power Flow (Newton)
Newton's method power flow (power balance, polar) converged in 3 iterations.
Converged in 0.01 seconds
================================================================================
| System Summary |
================================================================================
How many? How much? P (MW) Q (MVAr)
--------------------- ------------------- ------------- -----------------
Buses 14 Total Gen Capacity 400.0 -112.0 to 150.0
Generators 5 On-line Capacity 400.0 -112.0 to 150.0
Committed Gens 5 Generation (actual) 226.4 49.8
Loads 11 Load 223.7 95.4
Fixed 11 Fixed 223.7 95.4
Dispatchable 0 Dispatchable -0.0 of -0.0 -0.0
Shunts 2 Shunt (inj) -0.0 35.3
Branches 20 Losses (I^2 * Z) 2.73 13.52
Transformers 20 Branch Charging (inj) - 23.8
Inter-ties 0 Total Inter-tie Flow 0.0 0.0
Areas 1
Minimum Maximum
------------------------- --------------------------------
Voltage Magnitude 1.010 p.u. @ bus 3 1.030 p.u. @ bus 2
Voltage Angle -9.48 deg @ bus 14 0.00 deg @ bus 1
P Losses (I^2*R) - 0.50 MW @ line 1-2
Q Losses (I^2*X) - 2.11 MVAr @ line 8-7
================================================================================
| Bus Data |
================================================================================
Bus Voltage Generation Load
# Mag(pu) Ang(deg) P (MW) Q (MVAr) P (MW) Q (MVAr)
----- ------- -------- -------- -------- -------- --------
1 1.030 0.000* 81.43 -21.62 - -
2 1.030 -1.764 40.00 30.44 21.70 12.70
3 1.010 -3.537 40.00 12.60 50.00 25.00
4 1.011 -4.410 - - 47.80 10.00
5 1.017 -3.843 - - 7.60 1.60
6 1.030 -6.453 30.00 20.99 15.00 7.50
7 1.022 -4.885 - - - -
8 1.030 -1.540 35.00 7.40 - -
9 1.022 -7.246 - - 29.50 16.60
10 1.016 -7.415 - - 9.00 5.80
11 1.019 -7.080 - - 3.50 1.80
12 1.017 -7.473 - - 6.10 1.60
13 1.014 -7.721 - - 13.50 5.80
14 1.016 -9.481 - - 20.00 7.00
-------- -------- -------- --------
Total: 226.43 49.80 223.70 95.40
================================================================================
| Branch Data |
================================================================================
Brnch From To From Bus Injection To Bus Injection Loss (I^2 * Z)
# Bus Bus P (MW) Q (MVAr) P (MW) Q (MVAr) P (MW) Q (MVAr)
----- ----- ----- -------- -------- -------- -------- -------- --------
1 1 2 50.10 -18.36 -49.60 14.29 0.503 1.53
2 1 5 31.33 -3.26 -30.83 0.17 0.500 2.06
3 2 3 17.79 4.11 -17.63 -8.00 0.158 0.67
4 2 4 28.02 0.46 -27.58 -2.69 0.433 1.31
5 2 5 22.09 -1.13 -21.83 -1.70 0.262 0.80
6 3 4 7.63 -4.40 -7.58 3.21 0.047 0.12
7 4 5 -25.97 -5.70 26.07 5.99 0.092 0.29
8 6 11 6.91 2.37 -6.86 -2.27 0.048 0.10
9 6 12 7.93 1.32 -7.86 -1.17 0.075 0.16
10 6 13 19.15 2.76 -18.92 -2.31 0.234 0.46
11 7 9 39.12 1.46 -39.12 0.15 0.000 1.61
12 9 10 5.67 5.40 -5.65 -5.35 0.019 0.05
13 9 14 13.17 -3.85 -12.94 4.34 0.229 0.49
14 10 11 -3.35 -0.45 3.36 0.47 0.009 0.02
15 12 13 1.76 -0.43 -1.75 0.44 0.007 0.01
16 13 14 7.17 -3.93 -7.06 4.16 0.111 0.23
17 4 7 4.12 -3.76 -4.12 3.83 -0.000 0.06
18 4 9 9.22 -1.06 -9.22 1.53 0.000 0.47
19 6 5 -18.99 7.03 18.99 -6.06 0.000 0.97
20 8 7 35.00 7.40 -35.00 -5.29 0.000 2.11
-------- --------
Total: 2.727 13.52
mpc_sol = m.pull("mpc") # retrieve the solution
One can also save the case to a MATPOWER .m file from Octave/MATLAB. Comment
in and run the following code:
# m.eval("savecase('case14_andes.m', mpc)")
Convert from MATPOWER#
system = from_matpower(m, 'mpc')
m.pull() won't work if one has run OPF in Octave/MATLAB because Oct2Py does not support custom class objects created by MATPOWER.
from _matpower() will read the individual fields to construct an mpc dict internally before creating a system.
Add dynamic data#
One can create an Excel file with dynamic data only and use the xlsx parser to load data into system:
from andes.io import xlsx
xlsx.read(system, andes.get_case('ieee14/ieee14_dyn_only.xlsx'))
<andes.system.System at 0x7f8684043520>
system.setup()
system.PFlow.run()
system.TDS.run()
<Fault 1>: Applying fault on Bus (idx=7) at t=1.0 sec.
<Fault 1>: Clearing fault on Bus (idx=7) at t=1.03333 sec.
True
system.TDS.plt.plot(system.GENROU.omega)
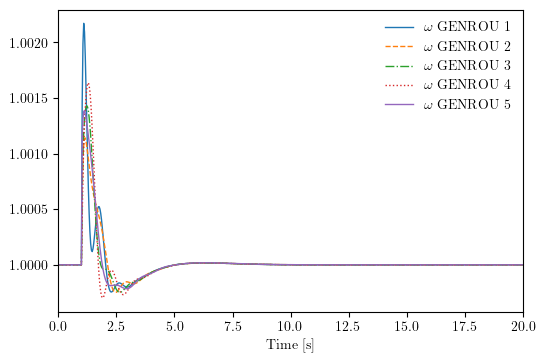
(<Figure size 600x400 with 1 Axes>, <AxesSubplot:xlabel='Time [s]'>)
Since the data in ieee14_dyn_only.xlsx is stripped from ieee14/ieee14_fault.xlsx, the above results is identical to the simulation of the latter case:
ss = andes.run(andes.get_case("ieee14/ieee14_fault.xlsx"),
routine='tds', verbose=30,
no_output=True, default_config=True)
<Fault 1>: Applying fault on Bus (idx=9) at t=1.0 sec.
<Fault 1>: Clearing fault on Bus (idx=9) at t=1.1 sec.
-> Single process finished in 0.7220 seconds.
ss.TDS.plt.plot(ss.GENROU.omega)
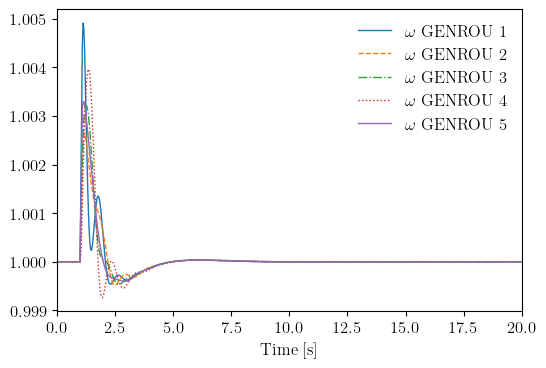
(<Figure size 600x400 with 1 Axes>, <AxesSubplot:xlabel='Time [s]'>)